仿射变换

对图形进行平移、旋转和缩放，
这样的操作称为 变换（transformations），
或 仿射变换（affine transformations）

平移

问题描述

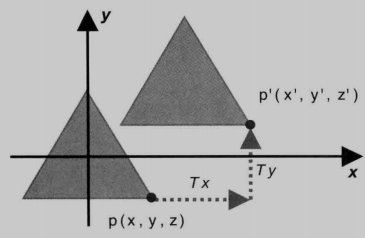
将点 p(x,y,z) 平移到 p’(x’,y’,z’),
在X轴、Y轴、Z轴三个方向平移的距离分别为：Tx，Ty， Tz ，
其中 Tz=0 。

等式

x’ = x + Tx
y’ = y + Ty
z’ = z + Tz

图解
着色器

平移是一个 逐顶点操作（per-vertex operation），
因此修改应当发生在 顶点着色器 。

Translated Triangle

TranslatedTriangle Code

TranslatedTriangle运行效果
TranslatedTriangle运行效果
TranslatedTriangle.html
TranslatedTriangle.js
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
<!DOCTYPE html>
<html lang="en">
<head>
  <meta charset="UTF-8">
  <meta http-equiv="X-UA-Compatible" content="IE=edge">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <title>Document</title>
  <script src="../examples/lib/cuon-utils.js"></script>
  <script src="../examples/lib/webgl-debug.js"></script>
  <script src="../examples/lib/webgl-utils.js"></script>
  <script src="./TranslatedTriangle.js"></script>
</head>
<body onload="main()">
  <canvas id="webgl" width="300" height="300"></canvas>
</body>
</html>
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
// 顶点着色器
var VSHADER_SOURCE =
  `
    attribute vec4 a_Position;
    uniform vec4 u_Translation;
    void main(){
      gl_Position = a_Position + u_Translation;
    }
  `;
// 片元着色器
var FSHADER_SOURCE =
  `
    void main(){
      gl_FragColor = vec4(0.0,1.0,0.0,0.4);
    }
  `;
// 在x、y、z方向上平移的距离
var Tx = 0.5,
  Ty = 0.5,
  Tz = 0.0;
function main() { 
  let canvas = document.getElementById('webgl');
  let gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('获取上下文失败');
    return;
  }
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) { 
    console.log('着色器初始化失败');
    return;
  }
  // 设置点位
  var n = initVertexBuffer(gl);
  if (n < 0) {
    console.log('缓冲区初始化失败');
    return;
  }
  // 将平移距离传输给顶点着色器
  var u_Translation = gl.getUniformLocation(gl.program, 'u_Translation');
  if (!u_Translation) {
    console.log('变量获取失败');
    return;
  }
  gl.uniform4f(u_Translation, Tx, Ty, Tz, 0.0);

  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  gl.clear(gl.COLOR_BUFFER_BIT);
  gl.drawArrays(gl.TRIANGLES, 0, n);
}

function initVertexBuffer(gl) {
  let vertices = new Float32Array([
    0.0, 0.5,
    -0.5, -0.5,
    0.5, -0.5
  ]);
  let n = vertices.length / 2;
  let vertexBuffer = gl.createBuffer();
  if (!vertexBuffer) {
    return -1;
  }
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);
  let a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);
  gl.enableVertexAttribArray(a_Position);
  return n;
}

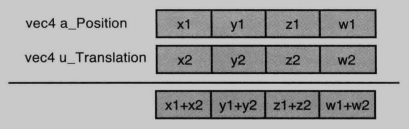
齐次坐标

gl.uniform4f() 需要接收 齐次坐标，
齐次坐标共有 4个分量，
最后一个分量如果是 1.0， 表示前三个分量是 一个点的三维坐标。

旋转

为了描述一次旋转，必须指明以下3个条件：

  • 旋转轴
  • 旋转方向
  • 旋转角度

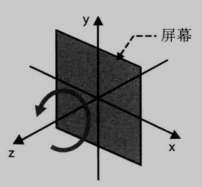
右手法则旋转（right-hand-rule rotation）

也称 正旋转，
判断标准就是：右手握拳，拇指朝上指向z轴正方向，其余四指指向的方向就是旋转的正方向。

数学表达

问题描述

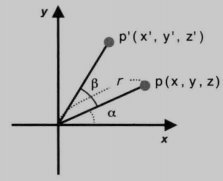
点 p(x,y,z) 旋转 β 角度之后变为了点 p’(x’,y’,z’),
旋转是绕Z轴逆时针进行的。

旋转等式

设 o 为原点
设 r = op
设 α 为 op 与 x轴夹角
x’ = rcos( α + β ) = r(cosαcosβ - sinαsinβ) = xcosβ - ysinβ
y’ = rsin( α + β ) = r(sinαcosβ + sinβcosα) = ycosβ + xsinβ
z’ = z

图解
着色器

依旧是由顶点着色器处理。

Rotated Triangle

RotatedTriangle Code

RotatedTriangle运行效果
RotatedTriangle运行效果
RotatedTriangle.html
RotatedTriangle.js
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
<!DOCTYPE html>
<html lang="en">
<head>
  <meta charset="UTF-8">
  <meta http-equiv="X-UA-Compatible" content="IE=edge">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">
  <title>Document</title>
  <script src="../examples/lib/cuon-utils.js"></script>
  <script src="../examples/lib/webgl-debug.js"></script>
  <script src="../examples/lib/webgl-utils.js"></script>
  <script src="./RotatedTriangle.js"></script>
</head>
<body onload="main()">
  <canvas id="webg" width="300" height="300"></canvas>
</body>
</html>
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
let VSHADER_SOURCE =
  `
  // x' = xcosb - ysinb
  // y' = xsinb + ycosb
  // z' = z
  attribute vec4 a_Position;
  uniform float u_CosB, u_SinB;
  void main(){
    gl_Position.x = a_Position.x * u_CosB - a_Position.y * u_SinB;
    gl_Position.y = a_Position.x * u_SinB + a_Position.y * u_CosB;
    gl_Position.z = a_Position.z;
    gl_Position.w = 1.0;
  }
  `;
let FSHADER_SOURCE =
  `
  void main(){
    gl_FragColor = vec4(0.0,1.0,0.0,0.4);
  }
  `;
let ANGLE = 90.0;
function main() { 
  let canvas = document.getElementById('webgl');
  let gl = getWebGLContext(canvas);
  if (!gl) {
    console.log('获取上下文失败');
    return;
  }
  if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {
    console.log('着色器初始化失败');
    return;
  }
  let n = initVertexBuffer(gl);
  if (n < 0) { 
    console.log('缓冲区初始化失败');
    return;
  }
  
  // 弧度制
  let radian = Math.PI * ANGLE / 180;
  let cosB = Math.cos(radian);
  let sinB = Math.sin(radian);

  
  let u_CosB = gl.getUniformLocation(gl.program, 'u_CosB');
  let u_SinB = gl.getUniformLocation(gl.program, 'u_SinB');
  if (!u_CosB || !u_SinB) {
    console.log('获取变量失败');
    return;
  }
  gl.uniform1f(u_CosB, cosB);
  gl.uniform1f(u_SinB, sinB);

  gl.clearColor(0.0, 0.0, 0.0, 1.0);
  gl.clear(gl.COLOR_BUFFER_BIT);
  gl.drawArrays(gl.TRIANGLES, 0, n);

}

function initVertexBuffer(gl) {
  let vertices = new Float32Array([
    0.0, 0.5, -0.5, -0.5, 0.5, -0.5
  ]);
  let vertexBuffer = gl.createBuffer();
  if (!vertexBuffer) {
    return -1;
  }
  gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer);
  gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STATIC_DRAW);
  let a_Position = gl.getAttribLocation(gl.program, 'a_Position');
  if (a_Position < 0) {
    console.log('获取变量失败');
    return -1;
  }
  gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0);
  gl.enableVertexAttribArray(a_Position);
  return vertices.length / 2;
}

一些小问题

关于uniform变量值的计算位置问题

一般将uniform变量放在JS中算好再传递到shader中，
这样只需要计算一次，效率更高。

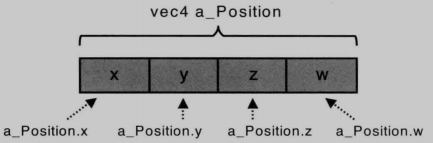
点操作符访问分量问题

在shader程序中，
无论是对 传入的变量 还是 gl变量，
都使用 点操作符 来访问分量。

弧度制参数问题

JS内置函数 Math.sin() 和 Math.cos()
都只接受 弧度制参数。
因此需要将 角度值参数 转换为 弧度制参数:

let radian = Math.PI * ANGLE / 180.0 ;

使用数组传入三角函数值

Vertex_Shader

1
2
3
4
5
6
7
8
9
10
11
let VSHADER_SOURCE =
  `
  attribute vec4 a_Position;
  uniform vec2 u_CosBSinB;
  void main(){
    gl_Position.x = a_Position.x*u_CosBSinB.x - a_Position.y*u_CosBSinB.y;
    gl_Position.y = a_Position.y*u_CosBSinB.x + a_Position.x*u_CosBSinB.y;
    gl_Position.z = a_Position.z;
    gl_Position.w = a_Position.w;
  }
  `;

传入uniform变量

1
2
let u_CosBSinB = gl.getUniformLocation(gl.program, 'u_CosBSinB');
gl.uniform2f(u_CosBSinB, cosB, sinB);

Rotated Triangle 升级版

蹦蹦床

程序中对u_sinB和u_cosB的赋值：
1
2
gl.uniform1f(u_sinB, Math.sin(currentAngle*Math.PI/180.0));
gl.uniform1f(u_cosB, Math.cos(currentAngle));
分享文章

快来参与讨论吧~